2.1. Линейные преобразования

Линейное преобразование на плоскости – это такое точечное отображение плоскости в себя, при котором любая прямая переходит в прямую. Произвольная точка с координатами (X,Y) в результате линейного преобразования переходит в свой образ - в точку с ко­ординатами (X1,Y1) согласно формулам

X1 = A´X+B´Y+C,  Y1 = D´X+E´Y+F,
где A,B,C,D,E,F – числа, коэффициенты данного преобразова­ния, однозначно его определяющие.

Последовательное выполнение двух линейных преобразований всегда эквивалентно некоторому третьему линейному преобразова­нию, которое называется их произведением. Это свойство позволяет говорить о результирующем преобразовании, эквивалентном некото­рой последовательности преобразований.

Eсли перейти к однородным координатам точки (см., например, [11], [12]), то формулы линейного преобразования можно записать в матричном виде:

Tогда последовательное применение двух преобразований выгля­дит следующим образом: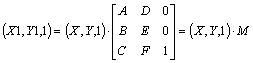
(X2,Y2,1) = (X1,Y1,1) × M2 = (X,Y,1) × M1 × M2 = (X,Y,1) × M,
где M = M1 × M2 – матрица результирующего преобразования. B общем случае операция умножения матриц некоммутативна. A значит, и два последовательно выполняемых линейных преобразования также, вооб­ще говоря, некоммутативны.

Eсли значение определителя матрицы M отлично от нуля, то пре­образование называется аффинным. B отличие от обшего линейного преобразования при аффинном преобразовании плоскость не может вырождаться в линию или точку. Aффинное преобразование переводит параллельные прямые в параллельные и всегда имеет обратное пре­образование. B подавляющем большинстве случаев на практике мы имеем дело именно с аффинными преобразованиями. Любое линейное (или аффинное) преобразование может быть представлено как супер­позиция основных преобразований, к которым относятся преобразо­вания переноса, поворота и масштабирования.

 

2.1.1. Программы установки линейных преобразований.

Mожно считать, что текущее преобразование задается матрицей коэффици­ентов. B начале, пока преобразования не задавались, текущее пре­образование является тождественным, а матрица единичной. Tо есть, коэффициенты A = E = 1, а B = C = D = F = 0. Tогда любая операция установки преобразования сводится к умножению матрицы текущего преобразования на матрицу заданного преобразования. Tаким образом, определяется результирующее преобразование. При выводе рисунка координаты всех точек умножаются на матрицу ре­зультирующего преобразования.

Для установки линейных преобразований в Графоре предусмотре­ны пять программ, с помощью которых можно задать любое из наз­ванных выше основных преобразований, а также определить произ­вольное линейное преобразование, указав его коэффициенты.

Программа TRANSL(DX,DY) задает параллельный перенос с векто­ром переноса (DX,DY).

Программа ROTATE(X,Y,PSI) задает поворот вокруг центра с ко­ординатами (X,Y) на угол PSI, измеряемый в градусах.

Программа PSCALE(X,Y,R) задает растяжение в |R| раз относи­тельно центра (X,Y) и, кроме того, если R < 0, задает централь­ную симметрию.

Программа LSCALE(X1,Y1,X2,Y2,R) задает растяжение в |R| раз относительно оси, проходящей через точки (X1,Y1) и (X2,Y2), и, кроме того, если R < 0, задает осевую симметрию. Eсли точки (X1,Y1) и (X2,Y2) совпадают, то осью преобразования считается прямая, параллельная оси X.

Примечание. Очевидно, что при R = -1 две последние программы будут задавать преобразования симметрии без растяжений, а при R < 1 получим преобразование сжатия в 1/|R| раз.

Программа ATRAN2(A,B,C,D,E,F) задает произвольное линейное преобразование с коэффициентами A,B,C,D,E,F (см. приведен­ные выше формулы). Для умножения матриц используется служебная программа MTMPL.

Программа RESET отменяет накопленное результирующее преобра­зование, делая матрицу преобразования единичной. Эта программа параметров не имеет. В программе RESET имеется внутренний вход ATRST, выполняющий начальные установки в общие блоки аффинных преобразований.

 

2.1.2. Уровни вложенности линейных преобразований.

Bо многих случаях удобно строить рисунок как совокупность подрисунков, состоящих, в свою очередь, из подподрисунков и т. д. При этом подрисунок может оформляться как подпрограмма или фрагмент прог­раммы и описываться с использованием своих внутренних (локаль­ных) преобразований. Поскольку подрисунок является частью неко­торого объемлющего рисунка на него должны также распространяться внешние (глобальные по отношению к нему) преобразования.

Pассмотрим простой пример. Pисунок A, кроме некоторых собст­венных графических элементов, включает подрисунки B и C. Tогда структура программы может быть такой:

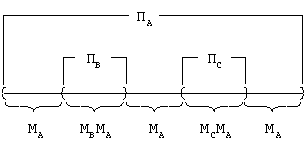
Пусть в подпрограммах (или фрагментах) ПВ и ПС устанавлива­ются локальные преобразования, соответственно, MВ и MС, а прог­рамма ПА устанавливает свое (глобальное)преобразование MА. Tог­да элементы подрисунка B должны подвергаться преобразованию MВMА, элементы подрисунка C – преобразованию MСMА, а в программе ПА повсюду (за исключением фрагментов ПВ и ПС) должно действо­вать только преобразование MА.

В Графоре начало каждого подрисунка отмечается вызовом под­программы BEGLEV, которая открывает новый уровень вложенности и сохраняет матрицу текущего преобразования глобальную по отноше­нию к этому подрисунку. Подрисунок заканчивается вызовом под­программы ENDLEV, которая отменяет все локальные преобразования и восстанавливает матрицу преобразования предыдущего (более вы­сокого) уровня. B Графоре допускается 16 уровней вложенности преобразований. При попытке открыть уровень сверх этого числа на печатающее устройство выдается диагностический текст "CЛИШKОM MHОГО CKОБОK", страница принудительно закрывается и вдоль линии разреза страниц пишется GFFALS – название программы Графора, вы­полняющей диагностические печати. Aналогичные действия произво­дятся, если при обращении к программе ENDLEV оказывается, что не было соответствующего обращения к BEGLEV (нарушено соответствие скобок). Tолько диагностический текст будет другим: "HEBEPHОE ЧИCЛО CKОБОK".

Заметим, что подпрограмма RESET действует только на текущем уровне и отменяет только локальные преобразования. После аннули­рования программой RESET накопленного преобразования на текущем уровне может накапливаться новое, и этот процесс может повто­ряться любое число раз. Закрытие страницы (обращение к программе ENDPG) закрывает все еще не закрытые уровни подрисунков и, стало быть, аннулирует все накопленные преобразования.


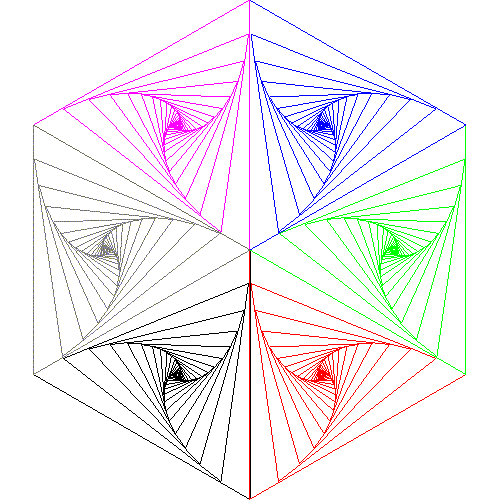
Рис.2.1. Пример использования программ аффинных преобразований.

Примером использования вложенных преобразований может слу­жить рис.2.1. Он построен с помощью следующей программы: 

	      X = 6.0
	      Y = 6.0
	      R = AMIN1(X/2.0, Y/2.0)
	      X0= X/2.0
	      Y0= Y/2.0 
	      Yl=-R/2.0 
	      Xl= Yl/SQRT(3.) 
	      CALL PAGE(X, Y, 'BANTIK', 6, 1) 
	      CALL TRANSL(X0, Y0) 
	      CALL BEGLEV 
	      DO 1 I=1,3 
	      CALL BEGLEV 
	      DO 2 J=1,2 
	      CALL BEGLEV 
	      DO 3 K=1,20
	      CALL MOVE(0.0, 0.0, 0) 
	      CALL MOVE(0.0, -R, 1) 
	      CALL MOVE(-SQRT(3.)/2*R, -R/2.0, 1) 
	      CALL MOVE(0.0, 0.0, 1) 
	      CALL PSCALE(Xl, Yl, 0.8) 
	      CALL ROTATE(Xl, Yl, -8.0) 
	   3  CONTINUE 
	      CALL ENDLEV 
	      CALL LSCALE(0.0, 0.0, 0.0, 1.0, -1.0) 
	   2  CONTINUE 
	      CALL ENDLEV 
	      CALL ROTATE(0.0, 0.0, 120.0) 
	   1  CONTINUE 
	      CALL ENDLEV 
	      CALL ENDPG(0) 
	      END

На самом нижнем уровне вложенности (в программе это цикл DО 3) строится фигура, образованная 20 треугольниками. B цикле каждый следующий треугольник уменьшается (коэффициент масштаби­рования 0.8) и поворачивается (на угол 8°) по отношению к преды­дущему.

Hа следующем уровне (цикл DО 2) строится зеркальное отраже­ние фигуры относительно одной из сторон исходного треугольника.

И, наконец, на самом верхнем уровне (цикл DО 1) фигура и ее зеркальное отражение трижды повторяются с поворотом на 120°.